Задача Вебера

Задача Вебера — одна из наиболее известных задач размещения производства. Названна в честь немецкого экономиста Альфреда Вебера. В задаче требуется найти точку на плоскости, которая минимизирует сумму цен перевозок из этой точки в n точек потребления, где для разных точек потребления назначается своя цена перевозки на единицу расстояния.

Задача Вебера обобщает поиск геометрической медианы, для которой цены перевозок полагаются равными для всех точек потребления, и задачу нахождения точки Ферма, геометрической медианы трёх точек. По этой причине задачу иногда называют задачей Ферма – Вебера, хотя то же самое имя используется и для задачи нахождения невзвешенной геометрической медианы. Задача Вебера, в свою очередь, обобщается задачей притяжения – отталкивания, которая позволяет отрицательные цены, так что для некоторых точек большее расстояние предпочтительнее.

Определение и история задач Ферма, Вебера и притяжения – отталкивания

	Задача Ферма	Задача Вебера	Задача притяжения – отталкивания
Сформулирована	Ферма (до 1640)	Симпсон (1750)	Телье (1985)
Геометрическое решение задачи треугольника	Торричелли (1645)	Симпсон (1750)	Телье (2013)
Прямое численное решение задачи треугольника	Телье (1972)	Телье (1972)	Телье (1985)
Итеративное численное решение задачи	Кун и Куэн (1962)	Кун и Куэн (1962)	Чен, Хансен, Жомар и Туй (1992)

В случае треугольника задача Ферма заключается в нахождении такой точки D по отношению к трём точкам A, B и C, что сумма расстояний от D до каждой из этих трёх точек была минимальна. Задачу сформулировал знаменитый французский математик Пьер Ферма до 1640. Задачу можно рассматривать как истинное начало задачи размещения производства. Торричелли нашёл геометрическое решение задачи около 1645 года, но прямого численного решения не было ещё более 325 лет. Кун и Куэн нашли итеративное решение общей задачи Ферма в 1962, а в 1972 Люк-Норманд Телье нашёл прямое численное (тригонометрическое) решение треугольной задачи Ферма. Решение Куна и Куэна пригодно для многоугольников с более чем тремя сторонами, что неверно для случая решения Телье по причинам, объяснённым далее.

Задача Вебера заключается в случае треугольника в нахождении такой точки D по отношению к трём точкам A, B и C, что сумма стоимости перевозки от пункта D до трёх остальных точек была минимальна. Задача Вебера является обобщением задачи Ферма, поскольку использует равные и неравные силы притяжения (см. ниже), в то время как в задаче Ферма силы одинаковы. Задача была впервые сформулирована и решена для случая треугольника Томасом Симпсоном в 1750. Кун и Куэн нашли итеративное решение в 1962, а решение Телье, найденное в 1972, применимо как к задаче Вебера, так и к задаче Ферма. Решение Куна и Куэна применимо к случаю многоугольника с более чем тремя сторонами.

В простейшем случае задача притяжения-отталкивания заключается в нахождении такой точки D по отношению к трём точкам A₁, A₂ и R, что приложенные силы притяжения точек A₁ и A₂ приложенная и сила отталкивания точки R компенсируют друг друга . Задача обобщает как задачу Ферма, так и задачу Вебера. Задачу сформулировал и решил для треугольника в 1985 Люк-Норманд Телье. В 1992 Чен, Хансен, Жомар и Туй нашли решение задачи Телье для многоугольников с более чем тремя сторонами.

Геометрическое решение Торричелли задачи Ферма для треугольника

Геометрическое решение Торричелли задачи Ферма для треугольника.

Геометрическое решение Эванджелиста Торричелли задачи Ферма для треугольника опирается на два наблюдения:

1. Точка D имеет оптимальное положение, если любой сдвиг с этой точки приводит к увеличению суммарного расстояния до точек A, B и C, что означает, что оптимальная точка — это только та точка, в которой бесконечно малый сдвиг в направлении к одной из трёх точек равен сумме изменений до двух других точек. Другими словами, точка D одинаково притягивается точками A, B и C.

2. В выпуклом четырёхугольнике, вписанном в окружность, противоположные углы в сумме дают 180°. Можно это сформулировать следующим образом: если мы рассечём окружность хордой AB, мы получим дуги окружности, скажем, AiB и AjB. Любой опирающийся на дугу AiB угол ∠AiB один и тот же для любой точки i, а опирающийся на дугу AjB угол ∠AjB один и тот же для любой точки j. Более того, углы ∠AiB и ∠AjB в сумме дают 180°.

Можно доказать, что из первого наблюдения следует, что в точке оптимума углы, в вершинах треугольников, опирающихся на отрезки AD, BD и CD, должны быть равны 360° / 3 = 120°. Из этого Торричелли пришёл к выводу, что:

1. Если из треугольника ABD, угол ∠ADB которого равен 120°, образован вписанный в окружность выпуклый четырёхугольник ABDE, угол ∠AEB треугольника ABE должен быть равен (180° − 120°)= 60°;

2. Один из способов получения точки D, для которой угол ∠ADB равен 120° — построить равносторонний треугольник ABE (поскольку все углы равностороннего треугольника равны 60°), где точка E расположена вне треугольника ABC, и построить окружность, вокруг этого треугольника. Тогда для всех точек D’ описанной вокруг треугольника окружности, лежащих внутри треугольника, угол ∠AD’B равен 120°;

3. То же самое можно сделать для треугольников ACD и BCD;

4. Это приводит к построению равносторонних треугольников ACF и BCG, где F и G лежат вне треугольника ABC, а также к построению двух других окружностей вокруг этих равносторонних треугольников. Все три окружности пересекаются в одной точке D и углы, опирающиеся на отрезки AD, BD и CD будут равны 120°, что доказывает оптимальное положение точки.

Геометрическое решение Симпсона задачи Вебера для треугольника

Геометрическое решение Симпсона задачи Вебера для треугольника.

Геометрическое решение Симпсона так называемой «задачи Вебера для треугольника» (которая была сформулирована Томасом Симпсоном в 1750) напрямую вытекает из решения Торричелли. Симпсон и Вебер подчёркивают факт, что в задаче минимизации перевозок выгода от приближения к точкам потребления A, B или C зависит от того, что везётся и за какую цену. Следовательно, выгода от приближения на некоторое расстояние меняется и углы ∠ADB, ∠ADC и ∠BDC больше не должны быть равны 120°.

Симпсон показал, что треугольники ABE, ACF и BCG, строящиеся аналогично решению Торричелли, где E, F и G расположены вне треугольника ABC, должны быть пропорциональны силам притяжения. В случае задачи Ферма треугольники были равносторонними, поскольку силы притяжения одинаковы

Решение таково:

1. В строящемся треугольнике ABE сторона AB пропорциональна силе притяжения _Cw в направлении к C, сторона AE пропорциональна силе притяжения _Bw в направлении к B, а сторона BE пропорциональна силе притяжения _Aw в направлении к A.

2. В строящемся треугольнике BCG сторона BC пропорциональна силе притяжения _Aw в направлении к A, сторона BG пропорциональна силе притяжения _Bw в направлении к B, а сторона CG пропорциональна силе притяжения _Cw в направлении к C;

3. Оптимальная точка D расположена на пересечении двух окружностей вокруг построенных треугольников ABE и BCG.

Третий треугольник ACF, где F находится вне треугольника ABC, может быть построена на стороне AC и можно построить третью окружность вокруг этого треугольника. Эта третья окружность пересекает две другие окружности в той же точке D.

Геометрическое решение Телье задачи притяжения — отталкивания

Геометрическое решение Телье задачи притяжения — отталкивания.

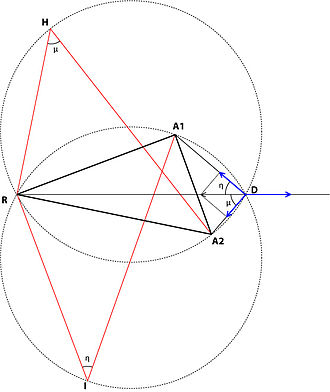
Для задачи притяжения — отталкивания в случае треугольника существует геометрическое решение. Оно было открыто относительно недавно. Это геометрическое решение отличается от двух предыдущих, поскольку в этом случае строящиеся треугольники сил накладываются на треугольник размещения точек A₁A₂R (здесь A₁ и A₂ — точки притяжения, а R — точка отталкивания).

Решение таково:

1. В строящемся треугольнике RA₂H, который накладывается частично на треугольник размещения точек A₁A₂R, сторона RA₂ пропорциональна силе притяжения _A1w в направлении к A₁, сторона RH пропорциональна силе притяжения _A2w в направлении к A₂, а сторона A₂H пропорциональна силе отталкивания _Rw в направлении от R.

2. В строящемся треугольнике RA₁I, который накладывается частично на треугольник размещения точек A₁A₂R, сторона RA₁ пропорциональна силе притяжения _A2w в направлении к A₂, сторона RI пропорциональна силе притяжения _A1w в направлении к A₁, а сторона A₁I пропорциональна силе отталкивания _Rw в направлении от R;

3. Оптимальная точка D располагается на пересечении двух описанных вокруг построенных треугольников RA₂H и RA₁I окружностей. Решение не получается, если одна из сил больше суммы двух других или если углы не сравнимы. В некоторых случаях нет вышеупомянутых нарушений (никакая сила не больше суммы двух других и углы сравнимы), но оптимальное решение находится в точке с большей силой притяжения.

Тригонометрическое решение Телье задач Ферма и Вебера

Углы задачи Вебера.

Случай несовпадающих вершин углов α.

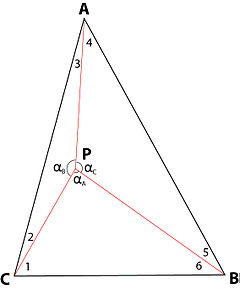
Более 332 лет отделяют формулировку задачи Ферма для треугольника и открытие неитеративного численного решения, хотя геометрическое решение существовало почти весь этот период времени. Объясняется это тем, что начала трёх векторов, направленных к трём точкам притяжения, могут не совпадать. Если они совпадают и лежат в оптимальной точке P, вектора в направлении к A, B и C и стороны треугольника точек притяжения ABC образуют шесть углов ∠1, ∠2, ∠3, ∠4, ∠5 и ∠6, а три вектора образуют углы ∠α_A, ∠α_B и ∠α_C. Легко выписать следующие шесть равенств, связывающих шесть неизвестных (углы ∠1, ∠2, ∠3, ∠4, ∠5 и ∠6) с шестью известными значениями (углы ∠A, ∠B и ∠C заданы, а значения углов ∠α_A, ∠α_B и ∠α_C зависят только от относительных значений трёх сил притяжения к точкам A, B и C):

∠1 + ∠2 = ∠C ;

∠3 + ∠4 = ∠A ;

∠5 + ∠6 = ∠B ;

∠1 + ∠6 + ∠α_A = 180° ;

∠2 + ∠3 + ∠α_B = 180° ;

∠4 + ∠5 + ∠α_C = 180°.

К сожалению, эта система шести уравнений является неопределённой и возможность начал трёх векторов в направлении точек притяжения объясняет, почему. В случае несовпадения легко видеть, что уравнения остаются верными. Однако оптимальное положение точки P исчезает ввиду треугольной «дыры» внутри треугольника. Фактически, как показал Телье (1972), эта треугольная «дыра» имеет в точности те же пропорции, что и «треугольники сил», которые мы строили в геометрическом решении Симпсона.

Чтобы решить задачу, нам следует добавить к указанным шести уравнениям седьмое, которое должно предотвратить появление треугольной «дыры» в центре треугольника точек притяжения. Другими словами, начала векторов должны совпадать.

Решение Телье задач Ферма и Вебера для треугольника осуществляется за три шага:

1. Определяем углы ∠α_A, ∠α_B и ∠α_C, при которых три силы притяжения _Aw, _Bw и _Cw уравновешивают друг друга, обеспечивая равновесие. Для этого используем следующие равенства:

cos ∠α_A = −( _Bw² + _Cw² − _Aw²) / (2 _Bw _Cw)  ;

cos ∠α_B = −( _Aw² + _Cw² − _Bw²) / (2 _Aw _Cw)  ;

cos ∠α_C = −( _Aw² + _Bw² − _Cw²) / (2 _Aw _Bw)  ;

2. Определяем значение угла ∠3 (это равенство обеспечивает совпадение точек D и E):

tan ∠3 = (k sin k’) / (1 + k cos k’) ;

где k = (CB/CA) (sin ∠α_B / sin ∠α_A), а k’ = (∠A +∠B + ∠α_C) − 180° ;

3. Решаем систему уравнений, в которой ∠3 уже известен:

∠1 + ∠2 = ∠C ;

∠3 + ∠4 = ∠A ;

∠5 + ∠6 = ∠B ;

∠1 + ∠6 + ∠α_A = 180° ;

∠2 + ∠3 + ∠α_B = 180° ;

∠4 + ∠5 + ∠α_C = 180°.

Тригонометрическое решение Телье задачи притяжения — отталкивания

Углы задачи притяжения — отталкивания для треугольника.

Случай несовпадения точек D и E.

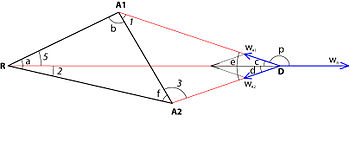
Телье (1985) расширил задачу Ферма – Вебера на случай отталкивающих сил. Рассмотрим случай для треугольника, в котором действуют две силы притяжения _A1w и _A2w и одна сила отталкивания _Rw. Здесь, как и в предыдущем случае, возможен случай несовпадения начал трёх векторов. Таким образом, решение должно требовать их совпадения. Тригонометрическое решение Телье этой задачи следующее:

1. Определяем угол ∠e:

cos ∠e = -( _A1w² + _A2w² − _Rw²) / (2 _A1w _A2w)  ;

2. Определяем угол ∠p:

cos ∠p = -( _A1w² + _Rw² − _A2w²) / (2 _A1w _Rw)  ;

3. Определяем угол ∠c:

∠c = 180° − ∠p ;

4. Определяем угол ∠d:

∠d = ∠e − ∠c ;

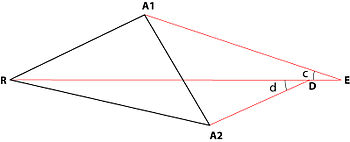
5. Определяем значение угла ∠3 (это уравнение требует совпадения точек D и E):

tan ∠3 = x / y ;

где x = sin ∠f – (RA₁/RA₂)(sin ∠d sin [∠e − ∠b] / sin ∠c) ; и y = (RA₁/RA₂)(sin ∠d cos [∠e − ∠b] / sin ∠c) − cos ∠f ;

6. Определяем угол ∠1:

∠1 = 180° − ∠e − ∠3 ;

7. Определяем угол ∠5:

∠5 = 180° − ∠b − ∠c − ∠1 ;

8. Определяем угол ∠2:

∠2 = ∠a − ∠5 .

Итеративное решение задач Ферма, Вебера и притяжения — отталкивания

Если число сил больше трёх, становится невозможно определить углы без рассмотрения геометрии многоугольника точек притяжения. Геометрические и тригонометрические методы бессильны. В этих случаях используются итеративные оптимизационные методы. Кун и Куэн (1962) предложили алгоритм, основанный на итерационном взвешенном методе наименьших квадратов обобщающий алгоритм Вайсфельда для невзвешенной задачи. Их метод работает для задач Ферма и Вебера, в которых есть много сил, но не для задачи притяжения-отталкивания. В этом методе для нахождения приближения к точке y, минимизирующей взвешенную сумму расстояний

$\sum _{i=1}^{n}w_{i}\,\|x_{i}-y\|,$

берётся начальное решение y₀ и на каждом шаге алгоритм приближается к оптимальному решению путём выбора y_j + 1, минимизирующего взвешенную сумму расстояний

$\sum _{i=1}^{n}{\frac {w_{i}}{\|x_{i}-y_{j}\|}}\|x_{i}-y\|^{2}$,

где начальные веса w_i делятся на расстояние от точки до приближения предыдущего шага. Каждая последующая аппроксимация может быть получена как взвешенное среднее единственного оптимального решения взвешенного метода наименьших квадратов:

$\left.y_{j+1}=\left(\sum _{i=1}^{n}{\frac {w_{i}x_{i}}{\|x_{i}-y_{j}\|}}\right)\right/\left(\sum _{i=1}^{n}{\frac {w_{i}}{\|x_{i}-y_{j}\|}}\right).$

Для задачи притяжения — отталкивания можно обратиться к помощи алгоритма, который предложили Чен, Хансен, Жомар и Туй (1992).

Интерпретация теории стоимости земли в свете задачи притяжения — отталкивания

В мире экономической теории использования пространства отталкивающие силы вездесущи. Стоимость земли является их главной иллюстрацией. Фактически существенная часть теория стоимости земли, как сельской, так и городской, может быть подытожена следующим образом.

В случае, когда всех привлекает единственная точка притяжения (сельский рынок или центральный деловой район города), соревнование различных участников торгов, желающих разместиться в центре, образует цену земли, которая преобразует точку притяжения системы в точку отталкивания, определяемую высокой стоимостью земли, и каждый житель и деловая активность размещается в точке, где силы притяжения и отталкивания компенсируются.

Задача притяжения — отталкивания и новая экономическая география

Оттавино и Тисс (2005) рассматривают задачу Телье как прелюдию «новой экономической географии» (НЭГ), разработанной в 1990-х годах, за которую Пол Кругман получил Нобелевскую премию по экономике в 2008 г. Концепция сил притяжения родственна концепции агломерации или центростремительных сил НЭГ, а концепция отталкивающих сил родственна концепции рассредоточения или центробежных сил.

Литература

• Pey-Chun Chen, Pierre Hansen, Brigitte Jaumard, Hoang Tuy. Weber's Problem with Attraction and Repulsion // Journal of Regional Science. — 1992. — Вып. 32.
• Harold W. Kuhn, Robert E. Kuenne. An Efficient Algorithm for the Numerical Solution of the Generalized Weber Problem in Spatial Economics // Journal of Regional Science. — 1962. — Вып. 4.

• Gianmarco Ottaviano, Jacques-François Thisse. New Economic Geography: what about the N? // Environment and Planning A. — 2005. — Вып. 37.
• Thomas Simpson. The Doctrine and Application of Fluxions. — London, 1750.
• Luc-Normand Tellier, Boris Polanski. The Weber Problem: Frequency of Different Solution Types and Extension to Repulsive Forces and Dynamic Processes // Journal of Regional Science. — 1989. — Т. 29, вып. 3. — С. 387–405.
• Luc-Normand Tellier. The Weber Problem: Solution and Interpretation // Geographical Analysis. — 1972. — Т. 4, вып. 3.

• Luc-Normand Tellier. Économie spatiale: rationalité économique de l'espace habité. — Chicoutimi: Gaëtan Morin éditeur, 1985.
• Luc-Normand Tellier. Sciences du territoire II : methodologies / Marc-Urbain Proulx. — Québec: Presses de l’Université du Québec, 2013.
• Alfred Weber. Über den Standort der Industrien. — Tübingen: J.C.B. Mohr, 1922.
  • Alfred Weber. The Theory of the Location of Industries. — Chicago: Chicago University Press, 1929.. Английский перевод

• Georges Wesolowski. The Weber problem: History and perspective // Location Science. — 1993. — Т. 1. — С. 5–23..

Ссылки

• Hazewinkel, Michiel, ed. (2001), "Weber problem", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4